
Klicken Sie das Bild an (98 kB).. |

Klicken Sie das Bild an (98 kB).. |
|
|
Allerdings mit dem einen Unterschied:
Ob Gerhard Mercator aus dieser Auseinandersetzung -1537 in Lissabon veröffentlicht - gelernt hat, weiß man bis heute (leider) nicht. Er hat sich auch selbst nie zu dieser Frage geäußert; daß aber die Arbeiten des Pedro Nunes in zwei Jahren von Lissabon über Antwerpen nach Löwen gekommen sein können, ist nicht auszuschließen. Wie dem auch sei: weder wurden die Seekarten durch die Kosmographen
aus nautischer Sicht
3 Da Gerhard Mercator sich
weder über die Konstruktion der Kugelloxodromen noch über die
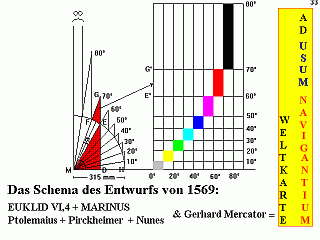
Herstellung seiner Weltkarte von 1569 AD USUM
NAVIGANTIUM - zum
Wie hat Gerhard Mercator "die Karte der wachsenden Breitenabstände" konstruiert?
Nur wenig später formulierte er den Ausgangspunkt kritischer Wissenschaftlichkeit
mit dem Gedanken: "In der gesamten Naturforschung
gilt ein Gesetz, das die Theorie zur Erklärung der
Im Verlaufe seines Vertrages erinnerte Hermann Wagner an die
"vergleichende Betrachtung von Karten mit Messung
derselben", "Kartometrie" genannt, die man nicht nur beim
infrage
Er selber übte diese Methode der Kartometrie dann auch 20 Jahre später, um das zweite große Rätsel der Kartengeschichte: die Entstehung der Weltkarte Gerhard Mercators, in Augenschein zu nehmen. Allerdings lag den Untersuchungen Hermann Wagners im Jahre 1915 kein Originaldruck der Weltkarte zugrunde. Aber auch seine Vorläufer in der Frage nach der Methode Gerhard Mercators: Arthur Breusing, Adolf Nordenskiöld, Siegmund Günther, wie seine Nachfolger Max Eckert, Paul Diercke, Fernand Marguet, Fontoura da Costa und Bruno Kyewski hatten keinen unmittelbaren Zugang zu dem am besten erhaltenen, nicht-kolorierten Exemplar gefunden, dem Baseler Exemplar der Mercatorkarte AD USUM NAVIGANTIUM von 1569. Breusing hatte 1869 von A.M. d'Avezac unvollständige Meßwerte erhalten, die am - damals einzig bekannten - Pariser Exemplar [P.E.] gewonnen worden waren. Marguet und Diercke, aber auch Nordenskiöld haben das P.E. ihren Überlegungen zugrunde gelegt, Marguet recht ungenau, Diercke mit größerer Akribie. Nordenskiöld dagegen versuchte - so hat es den Anschein nur einen rechnerischen Zugang; Günther und Fontoura schlossen sich den Überlegungen Nordenskiölds an; Kyewski folgte den Gedankengängen Marguets und Wagners. Wagner dagegen legte am Ende einer vergleichenden Betrachtung seinen kartometrischen Analysen im wesentlichen das Faksimile des damals noch vorhandenen - und 1889 entdeckten - Breslauer Exemplars zugrunde. Diese kartometrische Analyse Hermann Wagners zeigte dann auch in aller wünschenswerten Klarheit und Deutlichkeit, daß die Betrachtung vom Standpunkt der höheren Analysis nur dazu führen konnte, Gerhard Mercators Unternehmen als mehrfach reparatur-bedürftig hinzustellen: die - in der Tat vorhandenen, aber nebensächlichen und auf die Gesamtanlage sich nicht auswirkenden - (Stich-)Fehler wurden zum Teil nicht erkannt, nicht vorhandene Konstruktionsmängel wurden in einem theoretischen Konzept behoben, "aufgelöst". An der Leistung des Entwurfs durch Gerhard Mercator selbst zweifelte man zuerst einmal nicht. 5 Im Jahre 1917
brachte J. Drecker die Vermutung auf, daß schon Erhard
Etzlaub (spätestens) seit dem Jahre 1511
im Besitze der konstruktiven Möglichkeiten der später dann
6 Als D. Gernez 1937
in einer vergleichenden Untersuchung vor der Akademie der Belgischen Marine
alle bis dato vorgeschlagenen Lösungsansätze vortrug, wurde klar,
daß das
Hätte man - wie 1992 geschehen - das hervorragend erhaltene Baseler Exemplar einer genauen Messung unterzogen und bei den Rekonstruktionsversuchen den mathematischen Wissenstand Gerhard Mercators in Rechnung gesetzt - also wesentlich didaktische Fragen an die Geschichte gestellt -, so wäre man gewiß schon damals einer Lösung des Rätsels von 1569 nähergekommen. 7 Didaktische Überlegungen zur
unterrichtlichen Behandlung der Mercator-Projektion zeigten dann in der
Mitte der 60er Jahre - nachdem Bruno Kyewski, Schüler (des
Abiturjahrgangs 1930) und späterer
Lehrer am Mercator-Gymnasium in Duisburg, seine langjährigen Forschungen
über die Globus-Loxodromen zum 450. Geburtstag Gerhard Mercators
1962
Einen solchen Versuch hatte 1913 schon Josef Müller-Reinhard in der "Beilage zum Bericht über das Schuljahr 1912/13" des Königlichen Gymnasiums zu Duisburg veröffentlicht, - er arbeitete zu dieser Zeit als Autor der Kapitel über die geographisch-kartographischen und geomagnetischen Studien Gerhard Mercators an dessen zweiter, großer Lebensbeschreibung mit. Er lehnte sich - ohne ihn zu nennen - an den Vorschlag Arthur Breusings an, der in einer vorzüglichen Überlegung die 10°-Äquator-Länge - fälschlich - zu 54 mm rekonstruiert hatte, die d'Avezac ihm 1866 vergessen hatte mitzuteilen. Allerdings setzt dieser Rekonstruktionsversuch voraus, daß Gerhard Mercator die Trigonometrie der Sekansfunktion gekannt habe, - was - mit Gewißheit - nicht der Fall gewesen ist. 8 Zieht man geographiehistorisch längst bekannte Tatbestände zur Entstehung der See- und Weltkarten heran, so stößt man nicht erst bei Pedro Nunes auf die Fehlerhaftigkeit der Marinus-Plattkarten. Schon Ptolemäus hatte in seiner Geographie davon gesprochen, daß man die Verzerrungen in der Marinus-Abbildung der Oikumene dadurch abmildem könne, daß man an die Stelle der General-Karte, die die gesamte bekannte Welt (Oikumene) abbildet, Zonen-Karten ("klimatische" Karten) setzen könnte, die dadurch ausgezeichnet wären, daß wenigstens ihr Mittelparallel im richtigen Verhältnis zum Äquator(maß) stünde. Auch Nunes hatte diese Empfehlung an seine kartenentwerfenden Kosmographen weitergegeben, - aber keiner folgte ihm, so wie auch Ptolemäus seiner eigenen Empfehlung nicht nachkam: Schließlich schlug er im 24.Kapitel seiner Geographie zwei wesentlich andere Abbildungsarten als Marinus-Abbildungen vor. Diese Vorschläge wurde dann im 15. und 16. Jahrhundert in den großen "Ptolemäen", den gedruckten Ausgaben seiner Geographie, in die Tat umgesetzt; die Seekarten blieben von Marinus-Typus. Auf der Suche nach einem Verfahren, immer bessere Karten - insbesondere Seekarten - herstellen zu können, gelang Gerhard Mercator erst rund einVierteljahrhundert nach dem epochalen Erscheinen seines Erdglobus der weitere Durchbruch: Die Idee der Zonenplattkarte des Ptolemäus zusammen mit seinem Wissen um die Ähnlichkeitslehre des sechsten Buches der Euklid-Elemente führten ihn zur Entdeckung des normalachsigen winkeltreuen echten Zylinderentwurfs - wie die Kartographen heute sagen, schlichter und in Mercators Absicht gesagt: die Abbildung der Kugel AD USUM NAVIGANTIUM, was eben nicht mehr und nicht weniger bedeutet, als die doppeltgekrümmten Loxodromen der Kugel, die Kompaßgleichen, die alle Meridiane unter demselben Winkel schneiden, in der Ebene als Geraden mit derselben Eigenschaft abzubilden. 9 Marinus von Tyros - er "blühte" um 100 n.Chr. machte den Vorschlag, den Globus auf einen ihn im Äquator berührenden Zylinder ('normalachsig') abzubilden. Er verbesserte - nach Ptolemäus - seinen Vorschlag aber sogleich dadurch, daß er den Zylinder durch die Breite von Rhodos hindurchgehen ließ, so daß die Oikumene nicht von einem quadratischen, sondern von einem „echt" rechteckigen Netz von einander senkrecht schneidenden Meridianen und Breitenkreisen überzogen wurde. Nimmt man nun mit Gerhard Mercator den Lehrsatz Euklids zuhilfe:
so ist der vorstehenden Figur die Näherungskonstruktion der vergrößerten Breitenabstände unmittelbar zu entnehmen. Gerhard Mercator beschrieb selbst in der Legende An den geneigten Benutzer der Wehkarte den mathematischen Gehalt seiner Entdeckung - in Worten, wie es seine Art in mathematischen Dingen war - wie folgt: "Wenn drei Orte [in einer Plattkarte] auf derselben Seite des Äquators gelegen sind, so daß sie ein Dreieck bilden, und wenn die beiden äußeren zum mittleren in bezug auf Richtung und Entfernung gegeben sind, so ist es [in der Plattkarte der Seefahrer] ein Ding der Unmöglichkeit, daß auch diese beiden ihre gehörige Lage zueinander [richtig] erhalten.In diesen Sätzen liegt die vollkommen klare Einsicht in die Theorie wie die Praxis der 'normalachsigen, im Kleinsten ähnlichen echten Zylinderabbildung' offen zu Tage, - keiner der Altvorderen und keiner seiner Zeitgenossen konnte etwas Gleichwertiges bieten. In den Worten "haben wir allmählich vergrößert" (paulatim auximus) liegt einerseits die Größe, andererseits die Tragik des Unterfangens Gerhard Mercators: Er war sich im Klaren darüber, daß er - einerseits - in kleinen bis kleinsten Schritten vorzugehen hatte - und - andererseits - keinen "exakten Beweis" vorlegen konnte. Er ließ daher seinen ersten Biographen (und Nachbarn), Walter Ghim, 1595 sagen: Seine Lösung "entspricht der Quadratur des Kreises so trefflich, daß nichts zu fehlen scheint außer dem fehlenden Beweis - wie ich es mehrfach aus seinem eigenem Munde gehört habe." D. h. Gerhard Mercator sah sich außer Stande, seine Näherungskonstruktion
durch ein "exaktes" Verfahren zu ersetzen, - und teilte wohl deshalb der
wissenschaftlichen Mitwelt sein
|
 |
Eine nur auf die Idee der Proportion gegründete Konstruktion der
"vergrößerten Marinus-Breiten", eben der "Mercator-Breiten"
liefert die "Übersetzung" des o.a. Legendensatzes in die Sprache der
Mathematik:
D MED » D EGF
EG : EF » EF : MD EG » EF · ME / MD
ME = MH = MD · ME / MD.
|
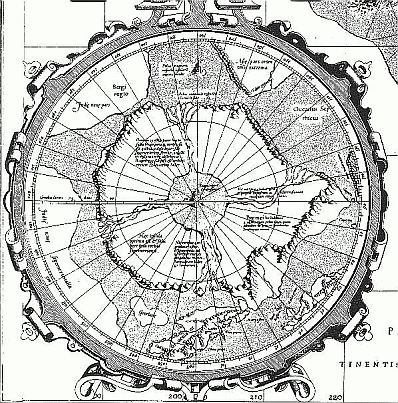 nen über das nördliche Polargebiet. Über den Südkontinent, dessen Existenz Gerhard Mercator aus naturphilosophischen Gründen glaubte ableiten zu können, über die terra australis, gab es damals noch keine Informationen; Australien war noch nicht entdeckt. Die mittelabstandstreue Azimutalprojektion stammt selbst nicht von Gerhard Mercator, obgleich sie ihm oft zugeschrieben wird. Juan Vespucci, ein Neffe des Amerigo Vespucci, benutzte sie 1524 zum ersten Mal. |
|
12 Die Lösung der nautischen Aufgaben hat Gerhard Mercator in den Legenden Brevis usus organi directorii (Kurze Einweisung in den Gebrauch der Kurstafel) und Distantiae locorum mensurandae modus (Die Methode Ortsdistanzen zu messen) aufgeschrieben. Er nimmt in diesen Anweisungen konstruktiv die Lösungen der näherungsweise rechnenden loxodromischen Trigonometrie seit Snellius (in Anschluß an Edward Wright 1599) vorweg. 1998: Erstaunlicherweise hatte John Dee schon im Jahre 1557 eine Zuordnung zwischen den Längen und den ihnen zugeordneten "vergrößerten" Breiten je Windstrich tabelliert, die aber in seinen Manuskripten im wesentlichen ein verborgenes Dasein führte, weil er mit ihrer Hilfe keine neue Plattkarte entwerfen wollte, sondern sie nur benutzte, um als advisor der Muscovy-Company das rechte Segeln unter Zuhilfenahme des Kompaß zu lehren.
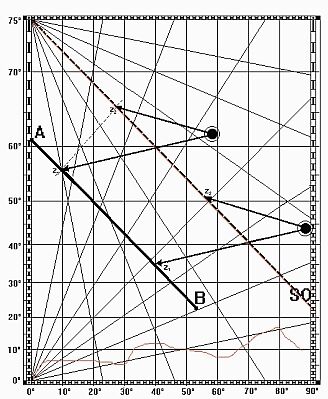 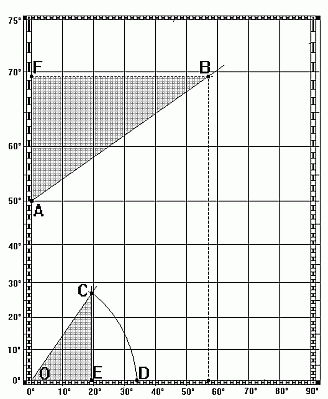 Diese Methode ist allgemeingültig - sagt Gerhard Mercator - , aber nicht immer die praktischste: Sollte der Kurs nahezu östlich gegen 90° (oder nahezu westlich gegen 270°) abgesetzt werden, so ist die Konstruktion von C recht unbestimmt wegen des "schleifenden Schnitts" in C. Gerhard Mercator empfiehlt dafür den Seeleuten dann die Methode der "Ausschöpfung durch die Mittelbreite": 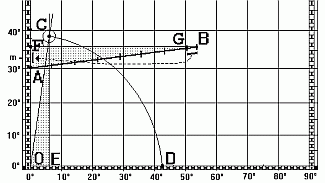 Wir tragen die (dann i.a. kleine) Breitendifferenz AF = D erschöpfend auf AB ab: G, mit AG = n • D. Den Rest GB messen wir, indem wir die Hälfte oberhalb, die Hälfte unterhalb der Mittelbreite m absetzen: G. Es folgt: AB = n • D + G.
 13 Steht die Analysis in der Gestalt der Integralrechnung zur Verfügung, so führt die Betrachtung der folgenden Figur dy = sec (b) · dbdessen Integration über [0 | j] auf y = ln ( tan [ p/4 + j/2 ] )führt. 14 Die Entwicklung der Land- und Seekarten führte schließlich dazu, daß auch die Geoid-Gestalt der Erde berücksichtigt wurde. C.F.Gauß deduzierte die Formeln für die konforme Abbildung des Erdellipsoids auf den transversalen Zylinder, der also gegenüber dem normalachsigen bei Mercator um 90° gedreht ist, aus den Differentialgleichungen der konformen Abbildung, ohne uns den Weg zu hinterlassen. Louis Krüger, weiland Direktor des Geodätischen Instituts in Potsdam, entwickelte dann in aller Breite die "Konforme Abbildung des Erdellipsoids in der Ebene", Potsdam 1912, und schuf damit die Grundlagen für die "Universale Transversale Mercatorabbildung" (UTM), die man kurz (bei uns) auch als "Gauß-Krüger-Abbildung" bezeichnet. Diese UTM liegt heutigentags allen Satelliten- und überhaupt deutschen geodätischen Landkarten zu Grunde: Eine Feststellung,die als posthume Ehrung Gerhard Mercators angesehen werden darf. Hat sein Kartenwerk ihn berühmt gemacht - sein Freund Abraham
Ortelius nannte ihn schon 1570
in humanistisch-hochlobender Rede nostri saeculi
Ptolemaius, den Ptolemäus unseres Zeitalters - , so hat
die
Weltkarte von 1569 AD USUM NAVIGANTIUM
ihn unsterblich gemacht.
|