Kugel Þ Ebene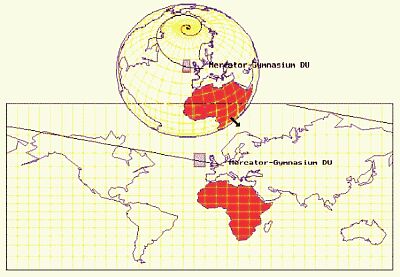 |
Kugel Þ Ebene |
| Wir stellen uns die folgenden Fragen:
A. Lassen sich Längen, Entfernungen, Abstände auf der Kugel verhältnisgleich in der Ebene nachbilden? D.h. ist eine betreffende Abbildung "längentreu"?
Nun hat die Einheitskugel das Gaußsche Krümmungsmaß l, die plane Ebene aber das Krümmungsmaß 0: quod non...
|
|
|
| Zur Konstruktion von Sternkarten auf Astrolabien wurde sie seit eh und je benutzt: |
|
|
| Ihre winkelerhaltende Eigenschaft hat aber keine sinnvolle Anwendung
außerhalb der Astronomie gefunden. (Die von Lietzmann behauptete
Seetauglichkeit ist in der Praxis nirgends anzutreffen.)
Eine winkeltreue Zylinderabbildung zu erfinden, stellte sich dem 15. und 16. Jahrhundert als Aufgabe, denn das Kompaß-orientierte Segeln der Entdecker auf hoher See machte eine Karte dieses Typs unbedingt erforderlich. Wir werden sehen: die Lösung der letzten Aufgabe liegt in Mercators Projektion.
Lamberts Karte ist im 20.Jahrhundert die Mutter der PETERS-Karten geworden, obgleich Peters davon offenbar nichts weiß - oder nichts wissen will. Später mehr davon. Teilen wir zunächst den Objektbereich KARTENENTWÜRFE nach den drei implizit schon eingeführten Merkmalen ein : |
|
azimutale Spezialfälle : orthographisch gnomonisch mittelabstandstreu flächentreu |
Unter dem erwähnten dreiteiligen Einteilungsprinzip gliedern sich
die Kartenprojektionstypen wie folgt:
Nimmt man eine weitere Einteilung nach der Linienart der Kartenmeridiane
und -parallelen vor, so unterscheidet man ECHTE von UNECHTEN Entwürfen:
Unechte Entwürfe eignen sich für Erdkarten oder auch für große Ausschnitte der Erdoberfläche. Der bekannteste unechte Entwurf - heute nach Bonne (1752)
genannt - hat eine jahrtausendalte Geschichte:
ÜBRIGENS: Ob wir "Entwurf "oder "Projektion" sagen, ist so ziemlich belanglose Deutschtümelei - um sich von den Franzosen zu unterscheiden. "Projektionen" der Darstellenden Geometrie (mit ihrer Perspektive) vorzubehalten, "Entwürfe" aber der allgemeinen Kartenlehre zuzurechnen, ist mathematisch wenig sinnvoll, da es sich in beiden Fällen - abgesehen von singulären Punkten - um eineindeutige Zuordnungen von Kugelpunkten zu Punkten der Ebene (umkehrbaren Abbildungen) handelt. |